Исследование аналоговых фильтров
Процедура синтеза электронного фильтра включает два основных этапа. Первым этапом является аппроксимация – процедура получения передаточной функции, с заданной точностью воспроизводящей заданные частотные или временные характеристики. Передаточная функция, найденная на этапе аппроксимации, затем реализуется электрической цепью.
Наиболее распространенными видами передаточных функций, используемых для получения заданных амплитудно-частотных характеристик, являются функции Баттерворта и Чебышева.
Передаточная функция фильтра нижних частот Баттерворта n-го порядка характеризуется выражением
![]() . (7.1)
. (7.1)
Амплитудно-частотная характеристика фильтра Баттерворта обладает следующими свойствами:
АЧХ фильтра монотонно убывает с ростом частоты. По этой причине фильтры Баттерворта называют фильтрами с максимально плоскими характеристиками. На рис. 15.4 показаны графики амплитудно-частотных характеристик фильтров Баттерворта 3 и 5 порядков. Очевидно, что чем больше порядок фильтра, тем точнее аппроксимируется АЧХ идеального фильтра нижних частот.
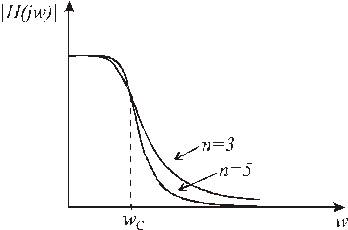
Рис. 7.2.1
Порядок передаточной функции n выбирают из условия обеспечения требуемого затухания в полосе задерживания на частоте ![]() . Модуль передаточной функции в полосе задерживания
. Модуль передаточной функции в полосе задерживания
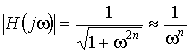 .
.
Порядок передаточной функции определяется приближенной формулой
![]() . (7.2)
. (7.2)
Здесь ![]() – частота в полосе задерживания, на которой задана величина затухания. Значение n, полученное с помощью формулы (15.5), округляется до ближайшего целого, большего n.
– частота в полосе задерживания, на которой задана величина затухания. Значение n, полученное с помощью формулы (15.5), округляется до ближайшего целого, большего n.
Пример 7.1. Определить порядок фильтра Баттерворта, у которого значение АЧХ на частоте, равной ![]() , не превышает 0.01.
, не превышает 0.01.
Решение. В соответствии с (7.2) ![]() . Округляя до ближайшего большего целого, получаем, что такое ослабление в полосе задерживания обеспечивает фильтр Баттерворта четвертого порядка.
. Округляя до ближайшего большего целого, получаем, что такое ослабление в полосе задерживания обеспечивает фильтр Баттерворта четвертого порядка.
Определяем координаты полюсов фильтра Баттерворта, полагая в (15.4) ![]() :
:
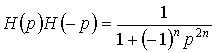 .
.
Приравняв полином знаменателя нулю, найдем, что полюсы фильтра Баттерворта с частотой среза ![]() расположены на окружности единичного радиуса на одинаковом угловом расстоянии друг от друга:
расположены на окружности единичного радиуса на одинаковом угловом расстоянии друг от друга:
![]() .
.
Каждая пара комплексных сопряженных полюсов образует множитель
![]() .
.
Квадрат модуля передаточной функции фильтра Чебышева определяется выражением
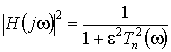 . (7.3)
. (7.3)
Здесь ![]() - полином Чебышева. Модуль передаточной функции фильтра Чебышева равен единице на тех частотах, где
- полином Чебышева. Модуль передаточной функции фильтра Чебышева равен единице на тех частотах, где ![]() обращается в нуль. График амплитудно-частотной характеристики фильтра Чебышева пятого порядка показан на рис. 7.3.
обращается в нуль. График амплитудно-частотной характеристики фильтра Чебышева пятого порядка показан на рис. 7.3.
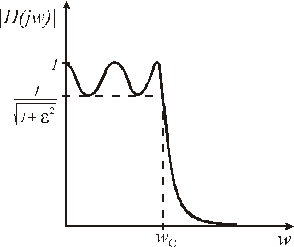
Рис. 7.3
Перечислим свойства частотных характеристик фильтров Чебышева.
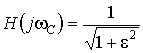 .
.
![]() .
.
Сравнение АЧХ фильтров Баттерворта и Чебышева показывает, что фильтр Чебышева обеспечивает большее ослабление в полосе пропускания, чем фильтр Баттерворта такого же порядка. Недостаток фильтров Чебышева заключается в том, что их фазочастотные характеристики в полосе пропускания значительно отличаются от линейных.
Для фильтров Баттерворта и Чебышева имеются подробные таблицы, в которых приведены координаты полюсов и коэффициенты передаточных функций различных порядков.
LC-фильтры были первыми фильтрами, которые использовались в устройствах передачи сигналов.
Пассивный фильтр, реализующий характеристики Баттерворта или Чебышева, представляет лестничную LC-цепь, включенную между резистивным сопротивлением источника сигнала и нагрузкой ![]() (рис. 7.4). Элементы фильтра рассчитывают таким образом, чтобы обеспечить передачу максимальной мощности в полосе пропускания.
(рис. 7.4). Элементы фильтра рассчитывают таким образом, чтобы обеспечить передачу максимальной мощности в полосе пропускания.
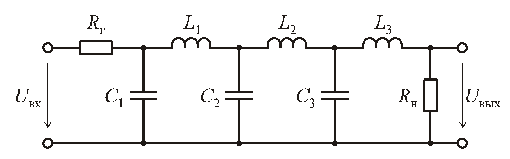
Рис. 7.4
С помощью лестничной LC-цепи можно реализовать только передаточные функции, нули передачи которых расположены на мнимой оси. Однако это не является серьезным ограничением, так как нули передачи частотно-селективных фильтров, как правило, расположены на мнимой оси, включая начало координат и бесконечность.
В простейшем случае нули передачи находятся в бесконечности. Таким свойством обладают передаточные функции фильтров нижних частот Баттерворта и Чебышева. Продольные ветви LC-цепи содержат индуктивности, а поперечные – емкости. Если нули передачи расположены в начале координат (фильтр верхних частот), то продольные ветви содержат емкостные элементы, а поперечные – индуктивные. Отличие фильтров Баттерворта и Чебышева в этом случае заключается только в разных значениях реактивных элементов, получаемых в процессе расчета. Количество реактивных элементов определяется порядком фильтра n.
Методы синтеза LC-фильтров хорошо разработаны. Существует обширная справочная литература, которая содержит данные о фильтрах различных порядков. Процедура расчета фильтра сводится к выбору типа и порядка фильтра.
Пассивные фильтры устойчивы, не требуют источников питания, имеют низкую чувствительность характеристик к изменениям номиналов элементов. Их основной недостаток при работе на частотах меньше 100 МГц – большие габариты и вес, обусловленные размерами индуктивных катушек.
В настоящее время во многих областях радиоэлектроники LC-фильтры почти вытеснены цифровыми и аналоговыми активнымиRC-фильтрами. Однако пассивные фильтры по-прежнему используются на частотах, превышающих 100 кГц.
Методы проектирования аналоговых фильтров с типовыми амплитудно-частотными характеристиками хорошо разработаны. Имеются многочисленные справочники, в которых приведены подробные таблицы с параметрами фильтров различных порядков. В табл. 7.1 и 7.2 приведены значения элементов нормированных фильтров Баттерворта и Чебышева с частотой среза 1 рад/с.
Таблица 7.2.1.
Значения элементов фильтров Баттерворта
n |
С1 |
L2 |
C3 |
L4 |
C5 |
L6 |
C7 |
L8 |
C9 |
2 |
1,4142 |
1,4142 |
|
|
|
|
|
|
|
3 |
1,0000 |
2,0000 |
1,0000 |
|
|
|
|
|
|
4 |
0,7654 |
1,8478 |
1,8478 |
0,7654 |
|
|
|
|
|
5 |
0,6180 |
1,6180 |
2,0000 |
1,6180 |
0,6180 |
|
|
|
|
6 |
0,5176 |
1,4142 |
1,9319 |
1,9319 |
1,4142 |
0,5176 |
|
|
|
7 |
0,4450 |
1,2470 |
1,8019 |
2,0000 |
1,8019 |
1,2470 |
0,4450 |
|
|
8 |
0,3902 |
1,1111 |
1,6629 |
1,9616 |
1,9616 |
1,6629 |
1,1111 |
0,3902 |
|
9 |
0,3473 |
1,0000 |
1,5321 |
1,8794 |
2,0000 |
1,8794 |
1,5321 |
1,0000 |
0,3473 |
Таблица 8.3.
Значения элементов фильтров Чебышева при Амакс = 1 дБ
n |
Rl |
C1 |
L2 |
C3 |
L4 |
C5 |
L6 |
C7 |
L8 |
C9 |
2 |
0,25 |
3,7779 |
0,3001 |
|
|
|
|
|
|
|
3 |
1,00 |
2,0236 |
0,9941 |
2,0236 |
|
|
|
|
|
|
4 |
0,25 |
4,5699 |
0,5428 |
5,3680 |
0,3406 |
|
|
|
|
|
5 |
1,00 |
2,1349 |
1,0911 |
3,0009 |
1,0911 |
2,1349 |
|
|
|
|
6 |
0,25 |
4,7366 |
0,5716 |
6,0240 |
0,5764 |
5,5353 |
0,3486 |
|
|
|
7 |
1,00 |
2,1666 |
1,1115 |
3,0936 |
1,1735 |
3,0936 |
1,1115 |
2,1666 |
|
|
8 |
0,25 |
4,7966 |
0,5803 |
6,1592 |
0,6005 |
6,1501 |
0,5836 |
5,5869 |
0,3515 |
|
9 |
1,00 |
2,1797 |
1,1192 |
3,1214 |
1,1897 |
3,1746 |
1,1897 |
3,1214 |
1,1192 |
2,1797 |
Как уже отмечалось, существуют многочисленные справочники, в которых приведены параметры фильтров, реализующих передаточные функции различных видов. Обычно это НЧ-структуры с частотой среза 1 рад/с. На практике такие фильтры совершенно бесполезны, так как для того или иного конкретного применения необходимы фильтры различных типов с частотами среза от единиц герц до сотен килогерц. Для получения фильтров с требуемыми характеристиками используют процедуру преобразования частоты. Исходный ФНЧ с частотой среза 1 рад/с является НЧ-прототипом. Частотное преобразование заключается в замене комплексной частотной переменной ![]() на новую переменную. С помощью частотных преобразований из нормированного НЧ-прототипа получают фильтры различных типов с требуемой частотой среза. Рассмотрим некоторые из этих преобразований.
на новую переменную. С помощью частотных преобразований из нормированного НЧ-прототипа получают фильтры различных типов с требуемой частотой среза. Рассмотрим некоторые из этих преобразований.
Преобразование НЧ–НЧ. Предположим, что нам необходим ФНЧ с частотой среза ![]() . Заменим частотную переменную в передаточной функции НЧ-прототипа на новую переменную
. Заменим частотную переменную в передаточной функции НЧ-прототипа на новую переменную
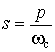 . (7.4)
. (7.4)
Это равносильно замене катушки, индуктивность которой равна L генри, катушкой индуктивностью ![]() генри. Конденсатор емкостью С фарад заменяется конденсатором
генри. Конденсатор емкостью С фарад заменяется конденсатором ![]() фарад. Сопротивления элементов денормированного фильтра на частоте
фарад. Сопротивления элементов денормированного фильтра на частоте ![]() будут такими же, как у нормированного фильтра на частоте
будут такими же, как у нормированного фильтра на частоте ![]() . Следовательно, преобразование (7.5) приведет к изменению масштаба по оси частот, и частота среза денормированного фильтра станет равна
. Следовательно, преобразование (7.5) приведет к изменению масштаба по оси частот, и частота среза денормированного фильтра станет равна ![]() .
.
Преобразование НЧ–ВЧ. В этом случае преобразование имеет вид
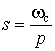 .
.
Здесь ![]() – частота среза фильтра верхних частот. При таком преобразовании передаточная функция ФНЧ-прототипа преобразуется в передаточную функцию ФВЧ с частотой среза
– частота среза фильтра верхних частот. При таком преобразовании передаточная функция ФНЧ-прототипа преобразуется в передаточную функцию ФВЧ с частотой среза ![]() . При этом конденсаторы заменяются катушками, индуктивность которых равна
. При этом конденсаторы заменяются катушками, индуктивность которых равна ![]() генри. Аналогично катушки заменяются конденсаторами емкостью
генри. Аналогично катушки заменяются конденсаторами емкостью ![]() фарад.
фарад.
Преобразование НЧ–ПФ. Это частотное преобразование трансформирует ФНЧ с одной полосой задерживания в полосовой фильтр с двумя полосами задерживания (рис. 15.7).
Преобразование ФНЧ-ПФ выполняется по формуле
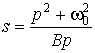 . (7.5)
. (7.5)
Здесь ![]() – центральная частота полосы пропускания;
– центральная частота полосы пропускания; ![]() ,
, ![]() – нижняя и верхняя частоты среза;
– нижняя и верхняя частоты среза; ![]() – ширина полосы пропускания.
– ширина полосы пропускания.
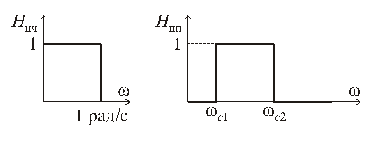
Рис. 7.5
Передаточная функция полосового фильтра, получаемая с помощью преобразования (7.5), имеет вдвое больший порядок, чем передаточная функция НЧ-прототипа.
Преобразование можно применить как к передаточной функции, так и к схеме исходного ФНЧ. При этом индуктивная катушка преобразуется в последовательное соединение катушки и конденсатора. Действительно, в соответствии с (15.8)
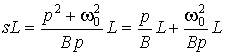 .
.
Этому равенству соответствует цепь, образованная последовательным соединением катушки индуктивностью ![]() генри и конденсатора емкостью
генри и конденсатора емкостью ![]() фарад. Аналогично конденсатор в ФНЧ-прототипе преобразуется в параллельную цепь, состоящую из конденсатора емкостью
фарад. Аналогично конденсатор в ФНЧ-прототипе преобразуется в параллельную цепь, состоящую из конденсатора емкостью ![]() фарад и катушки индуктивностью
фарад и катушки индуктивностью ![]() генри. В последних соотношениях С – емкость конденсатора в схеме НЧ-прототипа.
генри. В последних соотношениях С – емкость конденсатора в схеме НЧ-прототипа.
Нормирование по сопротивлению
В схемах НЧ-прототипа используются резисторы сопротивлением 1 Ом. Ясно, что на практике требуются фильтры с различными сопротивлениями нагрузки и генератора. При нормировании уровня сопротивления номиналы всех элементов схемы изменяют в определенное число раз. Например, если сопротивление нагрузочного резистора увеличивается в А раз, то индуктивности катушек также необходимо увеличить в А раз, а емкости конденсаторов – уменьшить в А раз. При этом частотные характеристики фильтра не изменятся.
Основной недостатокLC-фильтров, работающих в диапазоне частот менее 50 кГц – большие габариты и вес, обусловленные значительными размерами индуктивных катушек на этих частотах.
Этого недостатка лишены активныеRC-фильтры. Такой фильтр содержит резисторы, конденсаторы и активные элементы (как правило, операционные усилители). Активные фильтры широко используют в геофизической, медицинской аппаратуре, устройствах связи. В простых случаях активный фильтр представляет каскадное соединение звеньев второго-первого порядков (рис. 7.6).
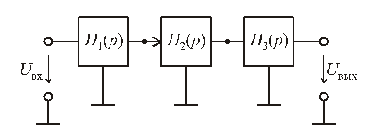
Рис. 7.6
Передаточная функция такого фильтра представляет произведение сомножителей второго порядка:
![]() .
.
Преимущества каскадной реализации заключаются в простоте расчета и настройки фильтра.
Рассмотрим подробнее передаточные функции звеньев второго порядка. В общем случае передаточная функция звена имеет вид
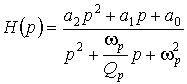 .
.
Параметры ![]() и
и ![]() определяют полюсы передаточной функции:
определяют полюсы передаточной функции:
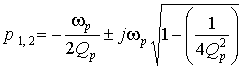 .
.
При ![]() полюсы
полюсы ![]() комплексно-сопряженные. Параметр
комплексно-сопряженные. Параметр ![]() называют частотой, а
называют частотой, а ![]() – добротностью реализуемой пары полюсов.
– добротностью реализуемой пары полюсов.
Коэффициенты числителя передаточной функции определяют расположение нулей передачи и соответственно тип передаточной функции. Передаточную функцию фильтра нижних частот получим, предположив ![]() :
:
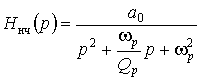 .
.
Нули передачи фильтра верхних частот расположены в начале координат, поэтому
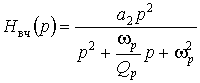 .
.
Передаточная функция полосно-пропускающего фильтра
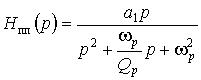 .
.
В практике проектирования активных фильтров используется большое число схем, реализующих передаточные функции первого и второго порядков. Простейшими являются схемы на одном ОУ с положительной обратной связью. На рис. 7.7 показан фильтр нижних частот Саллена – Ки. Он назван так по фамилиям инженеров П. Саллена и Э. Ки, предложивших первые практические схемы активных фильтров.
Операционный усилитель, резисторы ![]() и
и ![]() реализуют неинвертирующий усилитель с коэффициентом усиления
реализуют неинвертирующий усилитель с коэффициентом усиления ![]() . Передаточная функция фильтра
. Передаточная функция фильтра
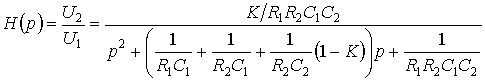 .
.
Для реализации фильтра верхних частот необходимо поменять местами резисторы ![]() ,
, ![]() и конденсаторы
и конденсаторы ![]() ,
, ![]() . Достоинства фильтра Салле-на – Ки – простота структуры, минимальное число активных элементов. Последнее особенно важно в тех случаях, когда необходимо уменьшить мощность, потребляемую фильтром.
. Достоинства фильтра Салле-на – Ки – простота структуры, минимальное число активных элементов. Последнее особенно важно в тех случаях, когда необходимо уменьшить мощность, потребляемую фильтром.
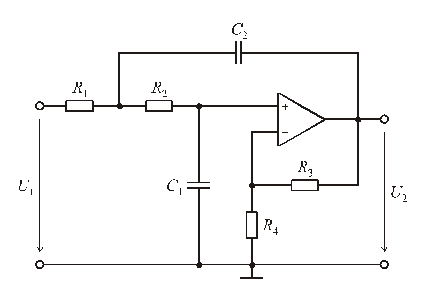
Рис. 7.7
В настоящее время разработаны различные процедуры расчета элементов фильтров Салена – Ки. Приведем один из вариантов, обеспечивающий равенство номиналов элементов. Исходными данными являются частота ![]() и добротность полюсов
и добротность полюсов ![]() . Расчет проводится в следующем порядке.
. Расчет проводится в следующем порядке.
![]() .
.
Коэффициент передачи усилителя
![]() .
.
Пример 7.2. Рассчитать фильтр нижних частот второго порядка, имеющий параметры: частота ![]() , добротность полюсов
, добротность полюсов ![]() .
.
Решение. Выбираем ![]() . Сопротивления резисторов
. Сопротивления резисторов ![]() . Коэффициент усилителя
. Коэффициент усилителя ![]() .
.
Для реализации передаточных функций полосно-пропускающих фильтров с невысокой добротностью полюсов (![]() ) используют звенья с многопетлевой обратной связью (рис. 7.8).
) используют звенья с многопетлевой обратной связью (рис. 7.8).
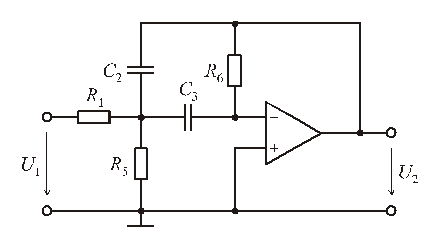
Рис. 7.8
Передаточная функция фильтра, показанного на рис. 7.8,
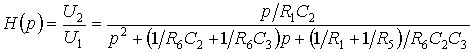 .
.
Расчет элементов схемы проводится в следующем порядке.
![]() ;
; ![]() ;
; ![]() .
.
В последних соотношениях ![]() – коэффициент передачи на частоте
– коэффициент передачи на частоте ![]() . Для упрощения схемы можно исключить резистор
. Для упрощения схемы можно исключить резистор ![]() , заменив его разрывом. Однако при этом нельзя будет контролировать коэффициент
, заменив его разрывом. Однако при этом нельзя будет контролировать коэффициент ![]() .
.
С помощью звеньев на одном ОУ можно реализовать и передаточные функции второго порядка с нулями передачи на мнимой оси. Однако такие звенья содержат большое число пассивных элементов. В частности, число конденсаторов может достигать трех-четырех. Значительно сложнее и процедуры расчета таких звеньев.
Главным недостатком звеньев на одном ОУ является высокая чувствительность характеристик к изменениям коэффициента усиления активного элемента. Особенно сильно это проявляется при реализации высокодобротных полюсов. В таких случаях используют звенья на нескольких ОУ. Их основные преимущества перед звеньями на одном ОУ заключаются в меньшей чувствительности характеристик, простоте регулировки и настройки. К тому же с точки зрения технологии интегральных схем минимизировать число активных элементов нецелесообразно. Поэтому звенья на нескольких ОУ часто оказываются более предпочтительными.
Универсальное звено на трех ОУ, реализующее одновременно передаточные функции ФНЧ, ФВЧ и ПФ, показано на рис. 7.9. Схема звена содержит два интегратора и сумматор. В зависимости от того, какой узел используется в качестве выходного, можно реализовать одну из трех передаточных функций:
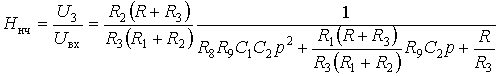 ; (7.6а)
; (7.6а)
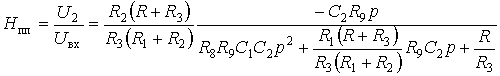 ; (7.6б)
; (7.6б)
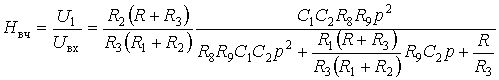 . (7.6в)
. (7.6в)
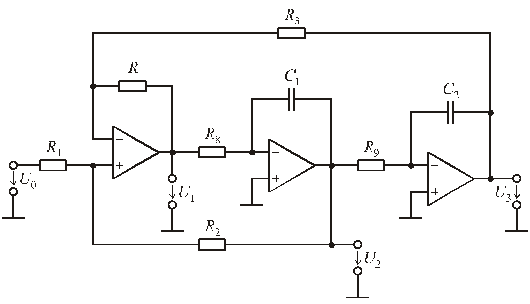
Рис. 7.9
Звенья на трех ОУ используют в универсальных модулях, изготавливаемых в виде интегральных схем. Такой модуль включает ОУ, конденсаторы и резисторы. Микросхема содержит внешние выводы для подключения источника питания, источника входного сигнала, а также регулировочных резисторов. С помощью таких резисторов можно регулировать характеристики фильтра (частоту ![]() и добротность полюсов
и добротность полюсов ![]() ). Модуль позволяет реализовать любую из передаточных функций (7.6).
). Модуль позволяет реализовать любую из передаточных функций (7.6).
При сборке схем активных фильтров использовать модели операционных усилителей LM324 или uA741 из библиотеки EVAL.slb. Примеры схем фильтров можно найти в файлах W7_2_1, W7_2_2, W7_2_3 в папке Electronics\Labs.